학교에서 들은 '알고리즘' 수업 정리입니다.
정렬 문제(Sorting Problem)란?
Input : n개의 대소를 가지는 숫자, 혹은 sequence (a₁, a₂, a₃, ... , a𝘯)
Output : 그러한 sequence의 순서를 바꾼 것 (a'₁, a'₂, a'₃, ... , a'𝘯) , permutation(reordering) (a₁ ≦ a₂ ≦ a₃ ≦ ... ≦ a𝘯)
주로 sequence는 배열에 저장되어 있고, aᵢ 는 key 이고 실제로는 각 key로 대표되는 satellite date가 있다.
(예 > 학번(key) + 이름, 성적 등의 정보(satellite data))

Pseudo code
Insertion-Sort(A)
for j = 2 to A.length
key = A[j] // j번째 원소 값
//Insert A[j] into the sorted sequence A[1... j-1].
i = j - 1 // i를 j-1부터 하나씩 줄여가면서 A[j]의 값을 넣어준다.
while i > 0 and A[i] > key // 키 값보다 A[i]의 값이 더 크면 A[i+1]에 A[i]를 넣어주기
A[i+1] = A[i]
i = i - 1 // 계속 해서 검토
A[i+1] = key // 마지막까지 검토를 했는데, A[i]가 더 작을때Is the Algorithm Correct?
Show the loop invariants(루프 불변성)
루프 불변성
: 알고리즘의 타당성을 증명하는 데 사용된다. 어떤 성질이 성립함을 증명할 때, 초기조건(initialization), 유지조건(maintenance), 종료조건(termination)이 성립함을 보이면된다.
초기조건 : j = 2 일 때, 부분 배열은 A[1]이고 정렬되어 있다.
유지조건 : 4-7행에서 A[j-1], A[j-2], A[j-3] ... 을 오른쪽으로 한 자리씩 이동시키고 A[j]를 적절한 위치에 삽입한다.
A[1 ... j-1]가 정렬되어 있었기 때문에 A[1 ... j] 는 정렬된 상태가 된다.
종료조건 : j = A.length + 1 일 때 끝나는데 이 때 유지조건에 의하여 A[1 ... A.length]는 정렬되어 있다.
Is the Algorithm Efficient?
(캐쉬나 가상 메모리와 같은 메모리 계층 구조가 없다고 가정)
알고리즘의 수행시간 = 수행된 기본연산(혹은 단계)의 갯수를 입력 크기 n 에 대한 함수로 나타냄

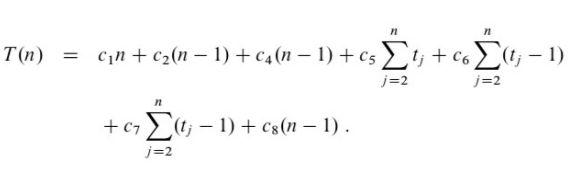
'알고리즘 공부' 카테고리의 다른 글
| 2. Recursion(2) (0) | 2022.09.16 |
|---|---|
| 2. Recursion(1) (0) | 2022.09.15 |
| 1. Insertion Sort 삽입 정렬(2) 프로그래머스 k번째수 [JS] (0) | 2022.09.02 |
| [알고리즘] 세 수 중 최솟값 구하기 / 삼각형 판별하기 (0) | 2022.05.14 |